Çözüm I:
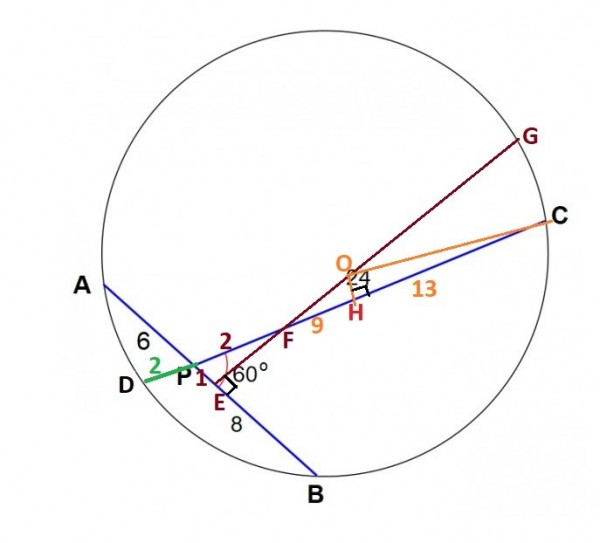
$CP$ nin uzantısı çemberi $D$ noktasında kessin.
$PA \times PB = PC \times PD$ (P noktasına göre kuvvet uygulayalım.)
$6 \times 8 = 24 \times PD$
$PD = 2$
$AB$ nin orta noktası $E$ olsun ve $E$ den çizilen orta dikme $CD$ yi F ve çemberi $G$ de kessin.
Bu takdırde $EP = 1$ ve $PF = 2$ olur.($\triangle FEP \space\space 30^{\circ} - 60^{\circ} - 90^{\circ}$ üçgeni)
Çemberin merkezi $O$, $EG$ üzerınde olur.(kirişten çizilen orta dikme merkezden geçer.)
$OH \perp CD$ çizelim. Bu takdirde $DH = CH =13$ ve $FH=9$ olur.
$OH = 3\sqrt3$ ($\triangle OHC \space\space 30^{\circ} - 60^{\circ} - 90^{\circ}$ üçgeni)
$R^2 = OC^2 = OH^2 + CH^2$
$R^2 = (3\sqrt3)^2 + 13^2=196$
$R=14$
Çözüm II:
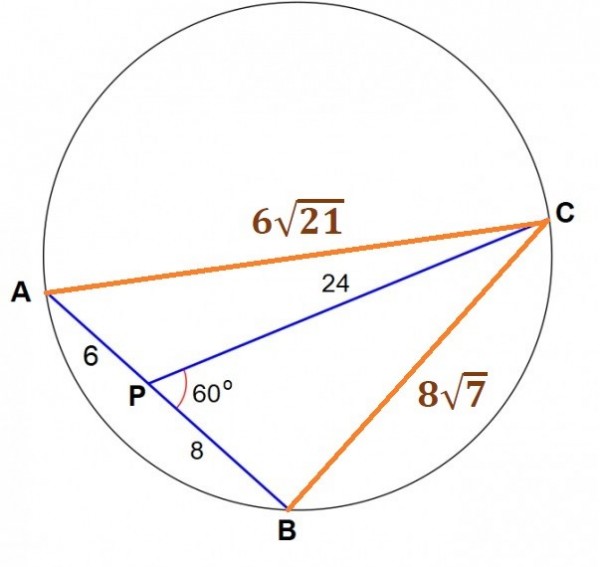
$\triangle ABC$ çizelim.
$AC^2 = 6^2 + 24^2 -2\times 6 \times 24 \times \cos 120^{\circ}$
$AC=6\sqrt 21$
$BC^2 = 8^2 + 24^2 -2\times 6 \times 24 \times \cos 60^{\circ}$
$BC=8\sqrt7$
$A(\triangle ABC)=\frac{14\times 6\sqrt{21} \times 8\sqrt7}{4R} = \frac{6 \times 24 \times \sin 120^{\circ} + 8 \times 24 \times \sin 60^{\circ}}{2}$
$R=14$
Çözüm III:
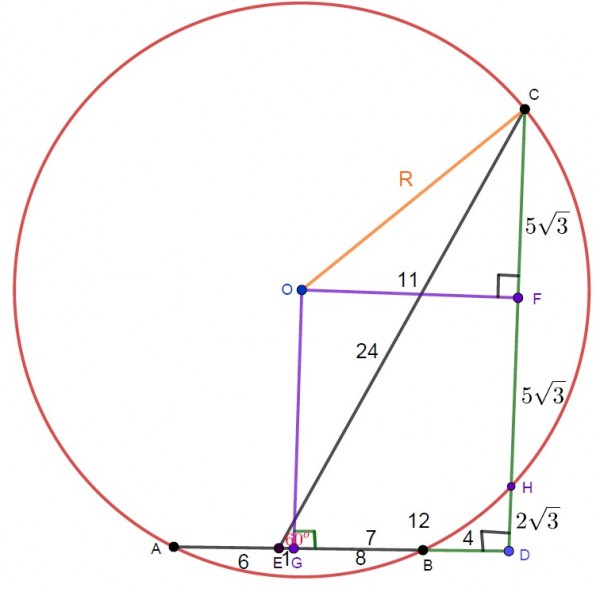
$BD \perp CD$ olacak şekilde $BD$ ve $CD$ yi çizelim.
$OG \perp AB$ ve $OF \perp CD$ çizelim.
Böylece $AG = BG, CF = HF$(Merkezden inilen dik, kirişi eşit böler)
$ED = 12, CD = 12\sqrt3$ ($\triangle CHO, 30^{\circ}-60^{\circ}-90^{\circ}$, üçgenidir.
$DB = 4, \space EG = 1, OF=GD = 11$
$DB \cdot DA = DH \cdot DC$ (D noktasına göre kuvvet uygulayalım.)
$4 \cdot 18 = DH \cdot 12\sqrt3, \space \text{ve}, DH = 2\sqrt3$
$ CF = HF = 5\sqrt3$
$R^2 = (5\sqrt3)^2 + 11^2$
$ R = 14 $