$sin^2x+cos^2x=1$
$sin\left(\dfrac{\pi}{2}-x\right)=cosx$
eşitlikleri bilinsin.
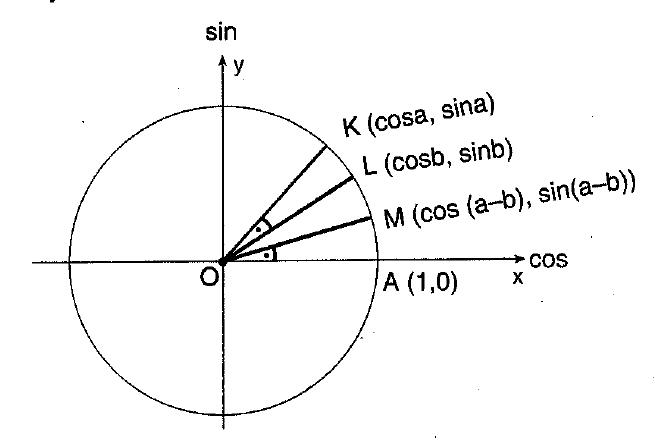
Birim çemberde;
$m(KOA)=a$ ve $m(LOA)=b$ olduğunda,
$m(KOL)=a-b$ dir.
$m(KOL)$'ına eşit olan $m(MOA)$'sı çizilirse,
$m(MOA)=a-b$ olur.
$m(KOA)=a$ ise $K(cosa,sina)$
$m(LOA)=b$ ise $L(cosb,sinb)$
$m(MOA)=a-b$ ise $M(cos(a-b),sin(a-b))$
$m(KOL)=m(MOA)$ ise $|KL|=|MA|$ dır.
$|KL|=\sqrt{(cosa-cosb)^2+(sina-sinb)^2}$
$|KL|^2=cos^2a-2.cosa.cosb+cos^2b+sin^2a-2.sina.sinb+sin^2b$ ve
$\to \quad |KL|^2=\underbrace{cos^2a+sin^2a}_1+\underbrace{cos^2b+sin^2b}_1-2.cosa.cosb-2.sina.sinb$
$\to \quad |KL|^2=2-2(cosa.cosb+sina.sinb)$ ($\star$)
$|MA|=\sqrt{(cos(a-b)-1)^2+(sin(a-b))^2}$
$|MA|^2=2-2cos(a-b)$ gelir.($\star\star$)
($\star$) ve ($\star\star$) taraf tarafa eşitlenirse,
$2-2cos(a-b)=2-2(cosa.cosb+sina.sinb)$ den
$\boxed{\boxed{cos(a-b)=cosa.cosb+sina.sinb}}$ gelir. $4.\Box$
kutu içindeki denklemde $-b=b$ dönüşümü yaparsak
$cos(a+b)=cosa.\underbrace{cos(-b)}_{cosb}+sina.\underbrace{sin(-b)}_{-sinb}$
$\boxed{\boxed{\to\quad cos(a+b)=cosa.cosb-sina.sinb}}$ $3.\Box$
$sin\theta=cos\left(\dfrac{\pi}{2}-\theta \right)$ eşitliğinden dolayı;
$sin(a-b)=cos\left(\dfrac{\pi}{2}-(a-b) \right)=cos\left(\left(\dfrac{\pi}{2}-a\right)+b \right)$
$\to \quad sin(a-b)=cos\left(\left(\dfrac{\pi}{2}-a\right)+b \right)$ olur
$\to \quad = \underbrace{cos\left(\dfrac{\pi}{2}-a\right)}_{sina}.cosb-\underbrace{sin\left(\dfrac{\pi}{2}-a\right)}_{cosa}.sinb$
$\boxed{\boxed{sin(a-b)=sina.cosb-sinb.cosa}}$ $2.\Box$
$sin(a-b)=sina.cosb-sinb.cosa$ özdeşliğinde $-b=b$ dönüşümü yaparsak;
$sin(a+b)=sina.\underbrace{cos(-b)}_{cosb}-cosa.\underbrace{sin(-b)}_{-sinb}$
$\boxed{\boxed{\to sin(a+b)=sina.cosb+sinb.cosa\quad }}$ $1.\Box$
İspatlar bitmiştir.