Lise de İçerme – Dışlama Prensibi ogretilip ogretilmedigini bilmedigim icin, lise icin zor bir soru olabilir. Katogori Lisans da olabilir.
$S=\{A,B,C,D,E,F\}$ ve ciftlerimiz $\{AB,CD,EF\}$olsun.
Hicbir kosul yokken tum durum $ 6!$ dir.
1 cift yanyana otursun:
$\{AB,C,D,E,F\}$ veya $\{A,B,CD,E,F\}$ veya $\{A,B,C,D,EF\}$
$3(5!\cdot2!)$
2 cift yanyana otursun:
$\{AB,CD,E,F\}$, $\{AB,C,D,EF\}$ veya $\{A,B,CD,EF\}$
$3(4!\cdot2!\cdot2!)$
3 cift yanyana otursun:
$\{AB,CD,EF\}$
$3!\cdot2!\cdot2!\cdot2!$
$\underbrace{6!}_{\text{Tum durumlar}}-\underbrace{3(5!\cdot2!)}_{\text{1 cift yanyana}}+\underbrace{3(4!\cdot2!\cdot2!)}_{\text{2 cift yanyana}}-\underbrace{(3!\cdot2!\cdot2!\cdot2!)}_{\text{3 cift yanyana}}=720-720+288-48=240$
Bu İçerme – Dışlama Prensibi olarak bilinir
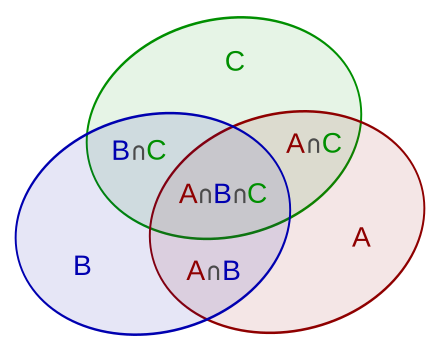
$|A\cup B\cup C|=|A|+|B|+| C|-|A\cap B|-|A\cap C|-|B\cap C|+|A\cap B\cap C|$
Tekrar sayma islemini duzeltme icin cikarma islemi yapilir.

Kume icindeki sayilar, alttaki islemi yaparken o alani kac defa saydigimizi gosterir.
https://en.wikipedia.org/wiki/Inclusion%E2%80%93exclusion_principle
Sizin sorunuz ise su sekilde olacak..
$\begin{align}|A\cup B\cup C\cup D|=&\Big(|A|+|B|+| C|+|D|\Big)\\-&\Big(|A\cap B|+|A\cap C|+|A\cap D|+|B\cap C|+|C\cap D|\Big)&\\+&\Big(A\cap B\cap C|+|A\cap B\cap D|+|B\cap C\cap D|\Big)&\\-&\Big(|A\cap B\cap C\cap D|\Big) \end{align}$