Soru 1[Orijinal Problem]: $7$ özdeş çorap ve $7$ özdeş ayakkabıya sahip $7$ kollu bir ahtapot, her ayakta bir çorap ve bir ayakkabı olmak üzere, kaç değişik şekilde (sekansta) tüm çorap ve ayakkabıları giyebilir. Not: Ayakkabının üzerine çorap giymek yok.
Çözüm:
Bu sorudan anladığım, çorap-ayakkabı giydirme işlemleri bittikten sonra görüntü olarak kaç farklı desen elde edileceğidir. (Metinde ''Sekans'' kelimesi var fakat bana birşey çağrıştırmıyor.) Önce çorapları her bir ayağa (kola/uzva) birer tane giydirmeliyiz. Bu yalnızca $1$ yolla olur. Çoraplar özdeş olduğu için hangi çorabın $1.$ ayakta olduğunun önemi yoktur. Şöyle de açıkayabiliriz: $7$ özdeş topu, $7$ farklı kutuya her kutuda birer tane top olacak biçimde kaç farklı yolla dağıtırız? Bunun da cevabı $1$ dir. Benzer biçimde ayakkabılar da özdeş olduğundan bunları da, her bir ayağa birer tane gelecek biçimde $1$ yolla giydiririz. Hangi ayağa hangi ayakkabının geldiğinin önemi yoktur. Dolayısıyla, çarpma prensibiyle istenen görüntülerin sayısı $1\cdot 1 =1$ dir.
Soru 2[Modifiye Problem]: $7$ farklı çorap ve $7$ farklı ayakkabıya sahip $7$ kollu bir ahtapot, her ayakta bir çorap ve bir ayakkabı olmak üzere, kaç değişik sıralamada tüm çorap ve ayakkabıları giyebilir. Not: Ayakkabının üzerine çorap giymek yok.
Not: Kişisel görüşüm burada doğru kelime ''sıralama'' dır ve ''sıralama'' kelimesine özellikle vurgu yapmak gerekli. (''Sekans'' kelimesi ile bu sıralamaya vurgu yapılmak istenmiş olmalı fakat okuyucuda o etkiyi bırakmıyor.) Aksi halde yorumlarda da belirtildiği gibi farklı anlamlar çıkarılabilir. Probleme açıklama olarak şunu da ekleyebiliriz: ''İlk çorabın $1.$ ayağa giyilerek başlanması ile ilk çorabın ikinci ayağa giyilerek başlanması farklı sıralamalar olarak sayılmaktadır''. Şimdi soruyu net biçimde ortaya koyduğumuzu düşünüyorum. (Halen sorudan farklı bir anlam çıkarıyorum diyen varsa yorum olarak ekleyebilir, ifadelerimizi daha da açık biçimde geliştirebilir miyiz diye yine bakarız.)
Çözüm: $i=1,2,\dots, 7$ olmak üzere $x_i$ ile $i$-inci ayağa çorap giyilmesini, $y_j$ ile $j$-inci ayağa ayakkabı giyilmesini gösterelim. Dolaysıyla bir yazılışta $x_i$, $y_i$ den önce görülmelidir. Soldaki iş sağdakinden önce yapıldığını göstermek üzere örnek bir sıralama: $x_1x_7x_3y_7x_4x_2y_2y_1x_6x_5y_5y_6y_3y_4$ yazılabilir. Hiçbir koşul olmadan bu $14$ nesneyi $14!$ yolla sıralayabiliyoruz. Fakat $x_1$, $y_1$'in solunda bulunacak, $x_2$, $y_2$'nin solunda bulunacak, ..., $x_7$, $y_7$'nin solunda bulunacak şekilde sıralamak istersek herbir işlem için $2$ ile bölmeliyiz. Aslında bu $x_i$ ile $y_i$ nin yer değiştirme sayısıdır. $2!$ de diyebiliriz. Diğer bir ifadeyle $x_i$ daima $y_i$ nin solunda bir konumda kalacaksa $x_i$ ile $y_i$ özdeş nesneler gibi alınarak sıralanmalıdır. Sonuç olarak tekrarlı permütasyonla
$$ \dfrac{14!}{2!^7} $$
elde edilir.
Not: Tekrarlı permütasyon fikrinin pekişmesi ve daha iyi anlaşılması açısından
1. 2016 da yazdığım Rick Grimes'ın Zombi Avı başlıklı problem. (O zamanlar The Walking Dead rüzgarı iyi esiyordu, sonra diziyi sıktılar.) Problemin cevabı, tekrarlı permütasyon fikriyle $\dfrac{9!}{3!2!4!}$ olur.
2. AIME (American Invitational Mathematical Examination) sınavlarından birinde sorulmuş bir soru diye hatırlıyorum ancak aramalarıma rağmen orijinal soruyu bulamadım. Çok önemli değil, kurgusu şöyleydi:
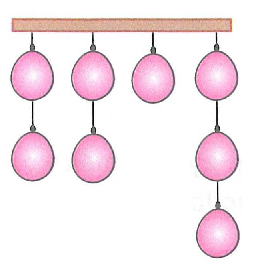
Aşağıdaki şekilde asılı olan özdeş $8$ balon vardır. Bir atıcı $8$ atış yaparak bu balonları patlatacaktır. Atıcı aynı ipte asılı olan balonlardan alttakini patlatmadan üsttekine atış yapmayacaktır. Patlayan balon ipten koparılmaktadır. Bu atıcı, her atışında bir balon patlatmak koşuluyla tüm balonları kaç farklı yolla patlatabilir? Cevap $\dfrac{8!}{2!2!1!3!}$ olur.
AIME problemini buldum. Şöye diyor:
3. [AIME 1990, Pr 8] Bir atış maçında, sekiz kil hedef, üçer hedeften oluşan iki asılı sütun ve iki hedeften oluşan bir sütun halinde düzenlenir. Bir nişancı, tüm hedefleri aşağıdaki kurallara göre kırmalıdır:
1) Nişancı önce hedefin kırılacağı bir sütun seçer.
2) Nişancı daha sonra seçilen sütunda kalan en düşük hedefi kırmalıdır.
Kurallara uyulursa, sekiz hedef kaç farklı sırada kırılabilir?

Çözümü verelim: Kil hedeflerin kırılma sırası $aaabbccc$ harflerinin tekrarlı permütasyonları ile bire bir eşleştirilebilir. Bunların sayısı da $\dfrac{8!}{3!\cdot 2! \cdot 3!} = 560$ olur.