Question

Pappus teoreminin bazı Öklidyen biçimlerini de bu başlıkta sorabiliriz:

 

Teorem 1. $\{ A, B, C \}$ ve $\{ A' , B' , C' \}$ nokta grupları, farklı iki doğru üzerinde olan altı farklı nokta olsun. O zaman $AB' \parallel A'B$ ve $BC' \parallel B'C$ ise $AC' \parallel A'C$ olduğunu kanıtlayınız.
 

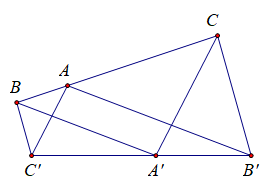
İspat: $\{ A, B, C \}$  ve $\{ A' , B' , C' \}$ nokta gruplarını taşıyan iki doğrunun kesişimi $D$ olsun.

Yukarıdaki her iki şekilde de $AB' \parallel A'B$ olduğundan $\dfrac{|DA|}{|DB|} = \dfrac{|DB'|}{|DA'|}$ ve 

$BC' \parallel B'C$ olduğundan $\dfrac{|DB|}{|DC|} = \dfrac{|DC'|}{|DB'|}$

olur. Bu iki eşitliği taraf tarafa çarparsak   $$\dfrac{|DA|}{|DC|} = \dfrac{|DC'|}{|DA'|}$$

olup kenar-açı-kenar benzerliğinden $AC' \parallel A'C$ elde edilir.

 

Notlar: 

1. Aslında bu ispatta da bir kusur vardır. $\{ A, B, C \}$  ve $\{ A' , B' , C' \}$ nokta gruplarını taşıyan iki doğru kesişmeyebilir ve $D$ noktası oluşmaz. Bu doğrular birbirine paralel olursa, Pappus teoreminin bir başka dejenere biçimini elde etmiş oluyoruz. $ABA'B'$ bir paralelkenar olur ve bu durumda $AC' \parallel A'C$ olduğunu görmek çok kolaydır.

2. Bu tür dejenere durumları da kapsayacak genel çözümler vermek için projektif geometrinin kavramları kullanılır. Örneğin; paralel iki (veya daha fazla) doğru sonsuzda bir noktada kesişir, denir. Örneğin $d_1\parallel d_2$ ise kesişim noktası $X$ olsun. Başka yönde paralel olan doğrular da sonsuzda başka bir noktada kesişir. $d_3\parallel d_4$ ise bunların kesişim noktası da $Y$ olsun. Bu tür $X$, $Y$ noktaları da sonsuzda bir doğru oluşturur: örneğin $\ell_{\infty}$ ile gösterilirse $X, Y \in \ell_{\infty}$ olur ...gibi.

3. Pappus teoreminin bazı ispatları BURADA verildi.

 

Şimdi ispatı (bence) Teorem 1'e göre daha zor olan bir diğer Öklidyen biçimli Pappus teoremininin kanıtını (Öklidyen yöntemler kullanmak şartıyla) soralım:

 

Teorem 2: $\{ A, B, C \}$ ve $\{ A' , B' , C' \}$ nokta grupları, farklı iki doğru üzerinde olan altı farklı nokta olsun. $BC' \cap B'C=Z$ ve $AC' \cap A'C = Y$ ve $AB' \parallel  A'B$ ise $YZ \parallel AB'$ olduğunu kanıtlayınız.

 

Comments

Teorm 1 in ispatını, B', A' ile C' arasında değil  iken de yapmalıyız.

O zaman, bu teoremden, genel (projektif düzlemde) Pappus Teoremi kolayca ispatlanıyor.

---

Doğan hocam Teorem 1 için $B'$; $A'$ ile $C'$ arasında olmayacak şekilde yeni çizimler de ekledim. $AB' \parallel A'B$ ve $BC' \parallel B'C$ şartlarını da sağlayacak biçimde; doğrulardan birinin üstündeki noktalar $A, B, C$ sıralamasında iken diğer doğrunun üstündeki noktalar ters sıralı olarak $C', B', A'$ biçiminde geliyor. Yine biri $B, A, C$ sıralamasında iken diğeri $C', A', B'$ ters sıralaması ile gelmiş oluyor. Yani $AB' \parallel A'B$ ve $BC' \parallel B'C$ şartları sağlanıyorsa daima ilgili doğrular üstündeki noktalar ters sıralı halde bulunmak zorundadır. Böyle bakınca,  şekillerde aynı varyasyonu incelediğimiz için Teorem 1'i iki durumda ele almamızın gerekliliğini tam anlayamadım. Gözden kaçırdığım başka çizim şekli mi var acaba? (Gerekli bir sebeple uyardığınızı düşünüyorum ama o sebebi henüz kavrayamadım, teşekkürler.)

Answer 1

Teorem 2'nin İspatı: Pappus teoreminin burada verdiğimiz ispatındaki benzer fikirleri kullanacağız. $A'B, B'C, C'A$ doğrularının meydana getirdiği üçgeni yine $PQR$ ile gösterelim.

$PQ \parallel AB'$ olduğundan $PQR \sim AB'R$ dir. Ayrıca $PQR$ üçgeninde sırasıyla $CYA', BZC'$ kesenleri için Menelaus teoremini uygulayalım:
$$\dfrac{RA}{AP}\cdot\dfrac{B'Q}{B'R}=1$$
$$\dfrac{QC}{CR}\cdot\dfrac{RY}{YP}\cdot\dfrac{PA'}{A'Q}=1$$
$$\dfrac{PB}{BQ}\cdot\dfrac{QZ}{FR}\cdot\dfrac{RC'}{C'P}=1$$

Bu üç ifadeyi çarparsak, $$\left (\dfrac{RA}{AP}\cdot\dfrac{PB}{BQ}\cdot\dfrac{QC}{CR}  \right )\left (\dfrac{RC'}{C'P}\cdot\dfrac{PA'}{A'Q}\cdot\dfrac{QB'}{B'R}  \right )\left (\dfrac{RY}{YP}\cdot\dfrac{QZ}{ZR}  \right )=1$$ olur. $A, B, C$ ve $A', B', C'$ noktaları doğrusal olduğundan $PQR$ üçgeninde Menelaus teoremi gereği ilk iki parantezdeki çarpımlar $1$'e eşittir. O halde üçüncü parantezdeki ifade de $1$'e eşittir. Buradan
$$\dfrac{RY}{YP}=\dfrac{ZR}{ZQ}$$ olup $PQR \sim YRZ$ (kenar-açı-kenar) benzerliği elde edilir. Böylece $A'B \parallel YZ$ bulunur.