$sin54=sin(9+45)=sin9.cos45+sin45.cos9=\dfrac{1}{\sqrt2}[sin9+cos9]$
$sin36=\dfrac{1}{\sqrt2}[sin9-cos9]$ buralarda kalsın
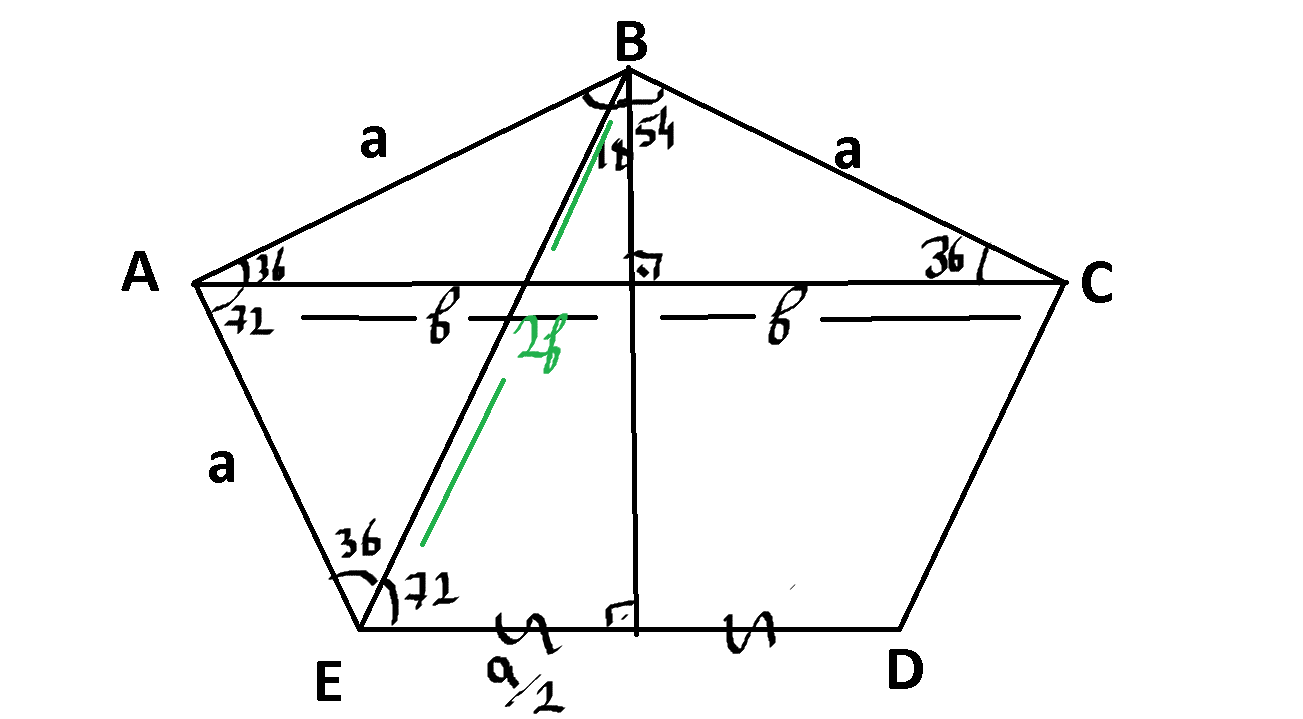
$sin36=\dfrac{\sqrt{a^2-b^2}}{a}$
$sin54=\dfrac{b}{a}$
$sin36=\dfrac{\sqrt{a^2-b^2}}{a}=\sqrt{\dfrac{a^2-b^2}{a^2}}=\sqrt{1-\dfrac{b^2}{a^2}}=\sqrt{1-sin^254}$
dolayısıyla
$sin54=\sqrt{1-sin^236}$ olur . Peki bize ne lazım?
$\dfrac{|AC|}{|AB|}=\dfrac{2b}{a}$ yani $2sin54$ lazım ozaman
$sin54=\sqrt{1-sin^236}=\sqrt{1-\dfrac{1}{2}[sin^29+cos^29-2sin9.cos9]}=\sqrt{\dfrac{1}{2}+\dfrac{sin18}{2}}=\dfrac{\sqrt{2+2.sin18}}{2}$
olur şimdi beşgende biraz oynayalım
$sin18=\dfrac{a}{4b}$ olur
$sin54=\dfrac{\sqrt{2+2.\dfrac{a}{4b}}}{2}=\dfrac{b}{a}$ burası düzenlenirse
$8.b^3-4a^2.b-a^3=0$ gelir bunu çözmek için
http://matkafasi.com/73409/%248y-3-4-x-2-y-x-3-0%24-denklemi-icin-cozum-yontemleri
buraya ,sercan hocanın ipucundan yola çıkıp çözümü ekliyeceğim oyuzden direk sadede gelelim.
$b=\dfrac{\sqrt5.a+1.a}{4}$ gelir
$\dfrac{|AC|}{|AB|}=\dfrac{2b}{a}=\dfrac{\sqrt5+1}{2}$ ispatlanır