Hanoi kulesi - Bulmaca

Question

"Tower of Hanoi" isimli bulmacada yapmamiz gereken $n$ uzunlugundaki kuleyi katlarin azalan yuksekligini bozmadan $A$ noktasindan $C$ noktasina tasimak...

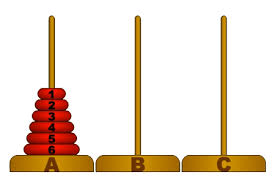
Eger $4$ birimlik bir kulemiz var ise asagidaki gif'teki gibi $15=2^4-1$ halede bunu basarabiliyoruz. Daha az hamlede basarmak mumkun mu? Daha genel olarak en az $2^n-1$ hamle ile bunu gerceklestirebilecegimizi gosteriniz.

Soruya isinmak icin bu internet sitesinden bu bulmacayi disk sayisini $3$ ile $8$ arasinda secip oynayabilirsiniz ya da cozumunu (Solve! butonuna) tiklayarak gorebilirsiniz.

Comments

sercan hocam özelden yazamıyorum malesef :).varmış oyle bır uygulama :D

---

tam soruyu yazıcaktım benden önce davranmış sercan hocam:)

---

Bir de algoritmasini sormustum, ona da bakabilirsin, cevabi yok henuz.

Answer 1

$n$ diski $A$'dan $C$'ye aktarmayı hedefleyen oyuna $(n)_{AC}$ ve bu oyunu kazanmak için gereken minimum hamle sayısına $s(n)_{AC}$ diyelim. $s(1)_{AC}=2^1-1=1$ ve $s(1)_{AC}=2^2-1=3$ olduğu aşikar. Şimdiyse $s(n)_{AC}=2^n-1$ ve $s(n+1)_{AC}=2^{n+1}-1$ için de sağlandığını ispatlayalım. Diyelim ki elimizde $(n+1)_{AC}$ oyunu var. İlk olarak $s(n)_{AB}$ hamle yaparak bir $(n)_{AB}$ oyunu oynamalıyız ki $(n+1)$. diski $C$'ye aktarabilelim. $(n)_{AB}$ oyununu oynadıktan sonra $(n+1)$. diski $C$'ye aktararak $1$ hamle daha yaparız. Ardından bu sefer de $s(n)_{BC}$ hamle yaparak bir $(n)_{BC}$ oyunu oynarsak $(n+1)_{AC}$ oyununu tamamlamış oluruz. $s(n)_{AC}=s(n)_{AB}=s(n)_{BC}=2^n-1$ olduğundan $s(n+1)_{AC}=1+s(n)_{AB}+s(n)_{BC}=1+2^n-1+2^n-1=2^{n+1}-1$ olmalıdır. Böylece sorudaki önermeyi tümevarımla ispatlamış olduk.