Bir fonksiyonun ve tersinin integrallerinin eşit olduğu bir durum.

Question

$f,\ [0,a]$ kapalı aralığında sürekli, kesin

azalan ve ${f(0)=b,f(a)=0}$ olacak şekilde bir fonksiyon olsun.

O zaman $\displaystyle \int_0^af(x)\ dx=\int_0^b f^{-1}(x)\ dx$

olduğunu gösterin.

Answer 1

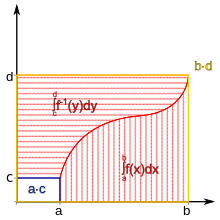
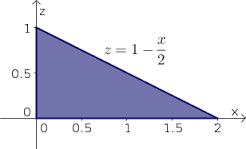
Wikipedia'dan asagidaki ilk resmi aldim. Sekilde $f$ fonksiyonu artan, fakat anlasilmasi icin koyuyorum. Eger bu azalan olursa sekil ikinci resme benzer olur. Bu soruda sunu deriz: ha alani $x$'e gore taramisiz, ha $y$'ye gore. Olay bu kadar basit.

Eger $a,b,c,d\geq0$ olacak sekilde ilki gibi alanimizi cizersek, fonksiyon $[a,b]$ araliginda azalan olsun, $f(a)=c$ ve $f(b)=d$ olsun.  Eger $(b-a)f(b)=(f(a)-f(b))a$ (yani $(b-a)d=(c-d)a$) olursa (ki soruda da bu saglaniyor) $x$'e gore taramak ile $y$'ye gore taramak arasinda bir fark olmaz. Aslinda yukaridaki esitlik sadece dikdortgenlerin alanlarinin esitligi. 

Comments

Bunun bir nedeni de fonksiyonla tersinin (eger varsa) her zaman $y=x$  dogrusununa gore simetrik olmasidir.

Answer 2

Analiz ile İspatı: 

Belirsiz İntegral tanımından ($\int f(x)\,dx=F(x)+C$ olmak üzere):  $$\int f^{-1}(x)\ dx=xf^{-1}(x)-F(f^{-1}(x))+C$$olduğu kolayca görülür. Diferansiyel-İntegral Hesabın Temel Teoremini kullanarak

$$\int_0^b f^{-1}(x)\  dx=\left.xf^{-1}(x)\right\vert_0^b-\left.F(f^{-1}(x))\right\vert_0^b=F(a)-F(0)=\int_0^af(x)\ dx$$elde  edilir.

Comments

Aslında burada örtülü olarak $f^{-1}$ in türevlenebildiği varsayımı var ama o olmadan da doğru olacağı Sercan ın çözümündeki gibi bir şekilden (veya integral tanımdan) gösterilebilir.

---

güzel çözüm ama kendim nasıl yaparım diye denedim, 1. eşitlik olan

$\displaystyle\int f^{-1}(x).dx=x.f^{-1}(x)-F(f^{-1}(x))+C$  'ı yapamadım


$f(x)=y$ gibi düşünüp sol tarafı $\displaystyle\int f^{-1}(x).dx=\displaystyle\int x.dx=x^2/2+C$ yaptım

sağ taraf ise;

$x.f^{-1}(x)-F(f^{-1}(x))+C=x^2-F(x)+C$  oldu ve eşitledim.

$\displaystyle\int x.dx=\dfrac{x^2}{2}=x^2-F(x)+C$     dedim   eşitliği görmek için türev aldım

$x=2x-F'(x)$                ($\int f(x)dx=F(x)+C$) varsayımınızdan ötürü

$x=f(x)$ buldum (ve tabiki hatalı)

$-----------------------$

2.denememde bunlara girmeden ;

$\displaystyle\int f^{-1}(x).dx=x.f^{-1}(x)-F(f^{-1}(x))+C$  bu ıfadenın turevını aldım

$f^{-1}(x)=f^{-1}(x)+x(f^{-1}(x))'-F'(f^{-1}(x)).(f^{-1}(x))'$ oldu ve düzenledim;


$x(f^{-1}(x))'=F'(f^{-1}(x)).(f^{-1}(x))'$          hertarafı  $(f^{-1}(x))'$'a bölüp sadeleştirebilir miyiz? evet ise devam ediyorum sadeleştirip;

$x=F'(f^{-1}(x))$ burada ne yapmam gerektiğini bilmiyorum.

$\int f(x)dx=F(x)+C$ tamam ama 

$\int f^{-1}(x)dx$'in F cinsinden eşiti nedir?

---

$\int f(x)\,dx=F(x)+C$ olması $F'(x)=f(x)$ demektir

$\begin{eqnarray} & &\frac{d}{dx}\left(xf^{-1}(x)-F(f^{-1}(x))+C\right)\\ &=& f^{-1}(x)+x(f^{-1})'(x)-F'(f^{-1}(x))\cdot (f^{-1})'(x)\\ &=&f^{-1}(x)+x(f^{-1})'(x)-f(f^{-1}(x))\cdot (f^{-1})'(x)\\ &=&f^{-1}(x)+x(f^{-1})'(x)-x\cdot (f^{-1})'(x)=f^{-1}(x)\end{eqnarray}$

---

$F'(f^{-1}(x))=f(f^{-1}(x))$  demekten şüphe etmiştim bu eşitlik her zaman sağlanır mı? ilginiz çok teşekkür ederim iyi günler sayın Hocam.