$\sum_0^\infty f(n) = \int_0^\infty f(x) dx + \frac{f(0)}{2} + i \int_0^\infty \frac{f(ix)-f(-ix)}{e^{2\pi x}-1}dx$

Question

Abel Plana formulunu cok sevdim paylasmak istedim ama soru formatinda olsun diye, yukaridaki esitlik hangi $f$ ler icin dogrudur? Belki ispatini da yapmak istersiniz.

Comments

analitiklik şartı kesin vardır

Answer 1

Eşitliğin son teriminden başlayalım yolculuğa. $ix=z$ ve $z'=-z$ olmak üzere bu terim

$$\begin{equation} \int_{x=0}^\infty dz \frac{f(z)-f(-z)}{e^{-i 2 \pi z}-1} = \int_{z=0}^{i \infty} dz \frac{f(z)}{e^{-i 2 \pi z}-1} + \int_{z'=0}^{- i \infty} dz' f(z') \frac{{e^{- i 2 \pi z'}}}{1-e^{- i 2 \pi z'}} = (1)\end{equation}$$ şeklinde ifade edilebilir.

İki zararsız varsayım yapacağız: $f(z)$ holomorfik bir fonksiyon olsun ve $|z| \xrightarrow{} \infty$ iken yeterince hızlı (ne kadar hızlı?) bir şekilde $f(z)\xrightarrow{} 0$ olsun. Bu durumda yukarıdaki integrandların yalnızca $z \in \mathbb{Z}$ noktalarında kutupları vardır.

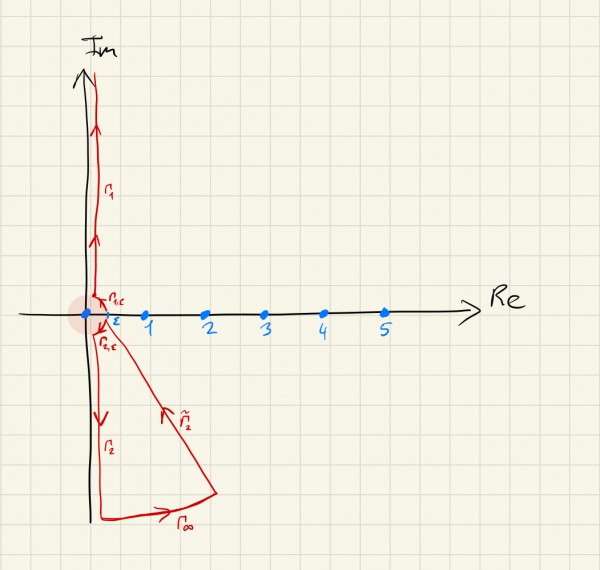
Bu integrallerin imajiner eksen üzerinde bir tekillikten geçtiğine dikkat ediniz. Dolayısıyla şimdi $(1)$ integralinin Cauchy esas değerini (principal value) karmaşık düzlemde 

$$(1) = \int_{\Gamma_1} \frac{f(z) dz}{e^{-i 2 \pi z}-1} +  \int_{\Gamma_2} \frac{f(z) \, e^{- i 2 \pi z} \, dz}{1-e^{- i 2 \pi z}}$$ kontur integralleri olarak yazabiliriz. Burada $\Gamma_{1,\epsilon}$ ve $\Gamma_{2,\epsilon}$ eğrileri orijin merkezli $\epsilon$ yarıçaplı bir çemberin üzerindeler. Hesap bittiğinde $\epsilon \xrightarrow{} 0$ limitini alacağız.

Şimdi $\Gamma_{2,\epsilon} \cup \Gamma_2 \cup \Gamma_\infty \cup \tilde \Gamma_2$  kapalı eğrisine odaklanalım. Cauchy integral teoreminden ve $\Gamma_\infty$ eğrisinin integrale katkı yapmamasından hareketle $\int_{\Gamma_2}=-\int_{\Gamma_{2,\epsilon} \cup \tilde \Gamma_2}$. Bu sayede üzerinde integral aldığımız eğileri aşağıdaki gibi yeniden çizebiliriz.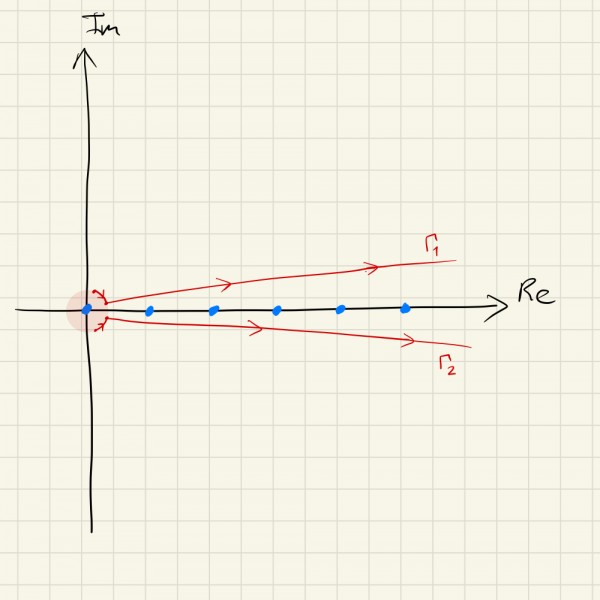 

Tekillikler yakınında dikkatli davranmak koşuluyla, biraz daha ileri giderek şöyle ilginç gözüken bir çizim de yapabilirdik.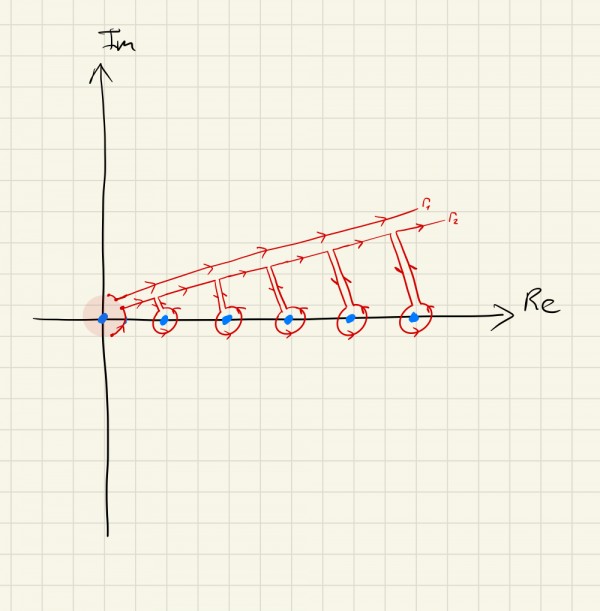

Şimdi $\Gamma_2$'nin integrandının gerekli kalıntılarını (residue) bulduktan sonra, $\epsilon \xrightarrow{} 0$ limitini de alınca sonunda elimize geçen:

$$\begin{aligned} (1) &= \frac{f(0)}{2} + \sum_1^\infty f(n) + \int_{z=i 0}^{i \infty} dz f(z) \frac{1-e^{-i 2 \pi z}}{e^{-i 2 \pi z}-1} \\ &= - \frac{f(0)}{2} + \sum_0^\infty f(n) + \int_{z=\epsilon}^{\infty} dz (\, -f(z) \,) \end{aligned}$$

Son adımda integrali reel eksene deforme ederken $f(z)$'nin holomorfik olmasından faydalandık.